几何拓扑学探索宇宙形状,从二维球面到四维时空,甚至高维机器人运动,绳结研究或解锁答案。
抬头看看四周,你可能会觉得脚下是个平坦的世界。毕竟,拿张地图就能逛遍陌生城市,纸是平的,路也好懂。这大概就是为什么古人一度相信地球是块平板。可如今,大多数人都明白,事实远非如此。你其实住在一个巨大的球面上,就像个地球大小的海滩球,表面还有些坑坑洼洼。这球面是个二维空间,你可以朝南北或东西走。
那还能住在什么别的空间里呢?比如,一个巨型甜甜圈的表面,也是个二维空间。数学家们通过几何拓扑学,研究所有可能的维度和空间。不管是设计传感器网络、挖掘数据,还是用折纸技术发射卫星,核心思路都离不开拓扑学。
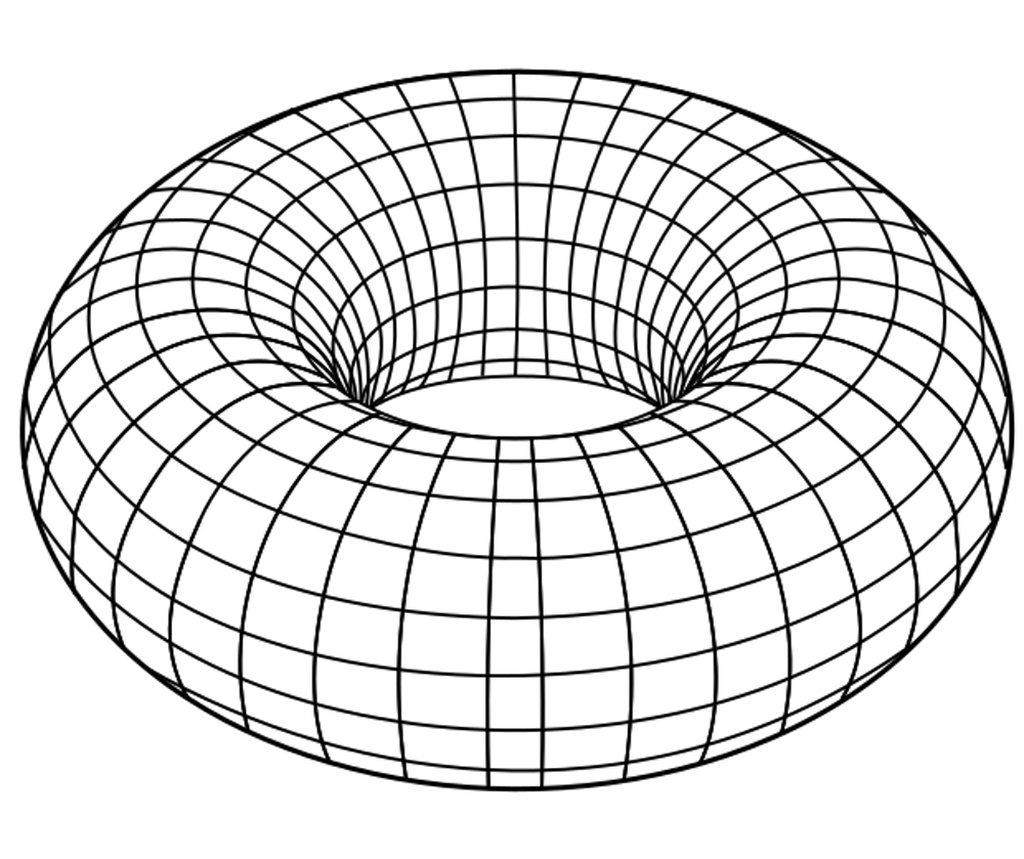
放眼宇宙,看起来是个三维空间,就像地球表面看起来是二维的。可要是把整个宇宙摊开来看,它可能比三维海滩球复杂得多,甚至更奇特。确定地球是个球体不需要拓扑学,但要搞清所有二维空间的可能性,这门学科就派上用场了。早在百年前,数学家们就摸透了所有二维空间的模样和特点。近几十年,他们又往前迈了一大步,对三维空间了解了不少。虽然还没像二维那样彻底弄明白,但已经足够让物理学家和天文学家试着推测我们到底住在怎样的三维空间里。
答案还没完全揭晓,但可能性多得让人兴奋。如果把时间算作一维,事情就更复杂了。想描述一颗彗星的位置,得用四个数字:三个定空间位置,一个定时间。这四个数字凑成了四维空间。于是,你可以开始想象,哪些四维空间是可能的,而你又住在哪一个里。
说到这儿,有人可能觉得,四维已经是极限了,干嘛还要考虑更高的维度?可弦理论却说,宇宙可能有远超四维的空间。现实中,高维也有用武之地。比如,想象三个机器人在仓库地板上跑来跑去。你在地上画个网格,用x和y坐标标记每个机器人的位置。三个机器人就需要六个数字来描述所有可能的站位,这就成了个六维空间。机器人多了,维度更高,再加上障碍物的位置,空间就更复杂了。要研究这个,得钻进高维空间的世界。
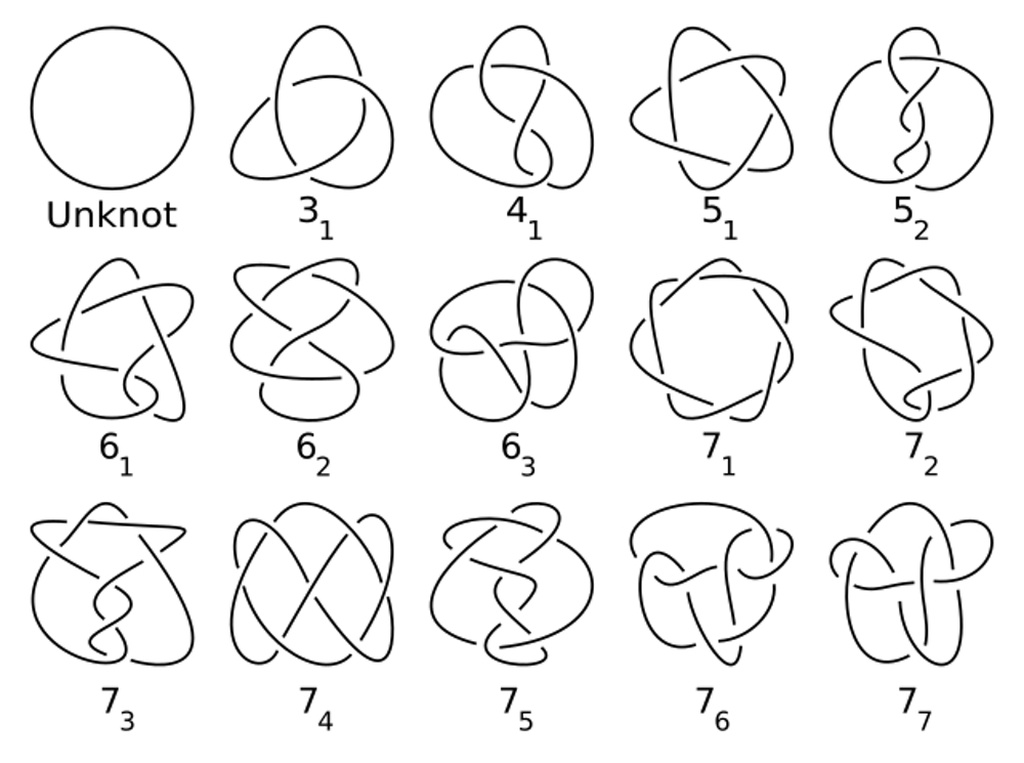
绳结是位于其他空间内部的空间的示例
绳结是拓扑学里的另一块宝地。拿根打结的绳子举起来,这是个一维空间(绳子本身)嵌在三维空间(你的房间)里。这种“数学结”最早从物理学里冒出来,现在成了拓扑学的核心。它们帮科学家理解三维、四维空间,结构奇妙又微妙,研究者们还在努力破解。比如,绳结在弦理论、DNA重组、化学中的手性都有大用场。
再想想工厂里的机器人。它们的运动轨迹可以用高维空间描述,就像行星和飞船的运行,或者大数据的“形状”。拓扑学无处不在,帮我们解开这些难题。宇宙到底什么形状?可能是球,也可能是甜甜圈,甚至更怪。几何拓扑学美妙又深奥,像四维庞加莱猜想这样的问题,探索最简单的封闭四维空间是什么;还有切片-丝带猜想,想弄清三维绳结和四维表面的关系。
这些谜题不光好玩,还实用。解开更多空间的秘密,能让我们更懂自己生活的世界,也能解决实际问题。你住的“形状”是什么?答案也许就藏在这些奇妙的数学里。
本文译自 ScienceAlert,由 BALI 编辑发布。
