走进科学
弦理论家意外发现无限多种计算圆周率的新公式
两位物理学家在研究基本力统一理论时,意外发现了多个计算圆周率的全新公式。
两位物理学家在试图开发一种统一基本力的理论时,意外发现了多个计算圆周率的新公式,这项研究发表在《物理评论快报》上。
Saha和Sinha不是数学家,他们本来并不是在寻找新的圆周率公式。这两位弦理论家原本在研究如何将电磁力、引力以及强核力和弱核力统一起来。在弦理论中,宇宙的基本构成单元不是粒子,而是像吉他弦一样振动的小线,这些振动产生了所有可见现象。在他们的研究中,Saha和Sinha探索了这些弦如何相互作用,并意外地发现了一些与重要数学量相关的新公式。
数千年来,人类一直试图确定圆周率的精确值,这并不奇怪,因为它在计算圆的周长和面积方面非常有用。即使在古代,学者们也开发了几何方法来计算这个数值。其中一个著名的例子是阿基米德,他通过多边形的方法来估算圆周率。他通过在圆内外分别绘制一个n边形,并计算它们的周长,得出了圆周率的一个近似值。
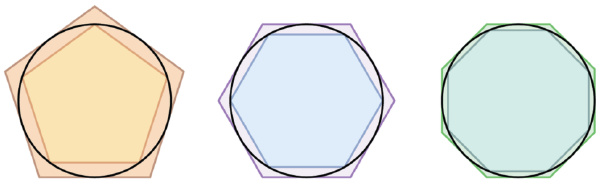
教师们通常会在学校教授这种方法。但即使你不记得,你也可以想象这个过程相当复杂。阿基米德甚至比较了具有96个顶点的多边形的周长,以证明圆周率在3.1408到3.1429之间。因此,这种方法并不是真正实用的精确计算圆周率的方式。
在15世纪,专家们发现了另一种表达圆周率的方式,即通过无穷级数来表示圆周率。通过逐项相加,可以得到圆周率的值。计算的项数越多,结果就越准确。

例如,印度学者Madhava发现,圆周率可以表示为4乘以一个从1开始、交替减去或加上分数的级数(如1/3、1/5等)。这个公式使得以非常简单的方式精确计算圆周率成为可能,但需要耐心。即使你计算了100项,仍然会与实际值相差较远。
Saha和Sinha在600多年后发现,Madhava的公式其实只是一个更通用的圆周率公式的特例。在他们的研究中,这两位弦理论家发现了如下公式:
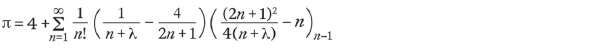
这个公式产生了一个无限长的和式。引人注目的是,它取决于一个可自由选择的参数λ。无论λ取何值,这个公式最终都能得到圆周率。而且,由于λ可以对应无限多的数值,Saha和Sinha因此发现了无限多种计算圆周率的公式。
如果λ无限大,该公式就会对应Madhava的公式。因为λ只出现在分数的分母中,所以对于λ=∞,相应的分数变为零(因为分母大的分数很小)。因此,当λ=∞时,Saha和Sinha的公式变为如下形式:

公式的前半部分已经类似于Madhava的公式:你在累加具有奇数分母的分数。然而,和式的最后一部分(–n)n – 1则不太熟悉。下标n – 1是所谓的Pochhammer符号。一般来说,表达式(a)n等于a x(a + 1) x (a + 2) x ... x (a + n – 1)。例如(5)3= 5 x 6 x 7 = 210。因此,上述公式中的Pochhammer符号为:(–n)n – 1 = (–n) x (–n + 1) x (–n + 2) x ... x (–n + n – 3) x (–n + n – 2)。
所有这些元素看起来很复杂,但它们可以快速简化。首先,从每个因子中减去–1。因此,如果n为奇数,巨大的乘积前面的符号是–1;如果n为偶数,则为+1。所以你得到(–n)n – 1 = (–1)n x n x (n – 1) x (n – 2) x ... x 3 x 2 x 1。
这个表达式实际上是(–n)n – 1 = (–1)nx n,结果如下:

经过几个步骤后,Saha和Sinha的公式就可以简化为Madhava的圆周率公式。换句话说,Saha和Sinha发现的公式实际上包含了Madhava的级数。
然而,Saha和Sinha报告称,对于较小的λ值,他们的公式计算圆周率要快得多。Madhava的结果需要100项才能得到与圆周率相差0.01的值,而Saha和Sinha的公式在λ=3时只需要前四项。作者在论文中写道:“当Madhava的级数需要50亿项才能收敛到10位小数时,新的表示方法在λ介于10和100之间时只需要30项。”不过,Saha和Sinha并没有找到计算圆周率的最有效方法,几十年来已知的其他级数可以更快地得到惊人的精确值。这件事真正令人惊讶的是,物理学家在其论文中旨在描述弦的相互作用时,意外地提出了一个新的圆周率公式。他们开发了一种方法来表示两个闭弦相互作用的概率——这是许多弦理论家几十年来一直在寻求的目标,但没有成功。
当Saha和Sinha仔细研究得出的方程时,他们意识到,他们不仅可以用这种方式表达圆周率,还可以表达黎曼猜想的核心——ζ函数,这是数学中最大的未解之谜之一。鉴于弦理论家的兴趣,他们的圆周率和ζ函数公式仅出现在论文的最后一段中。Sinha在Numberphile的YouTube视频中表示:“我们的动机当然不是为了找到一个圆周率公式。”他说,“圆周率只是一个副产品。”
本文译自 Scientific American,由 BALI 编辑发布。