Tech
一个著名的密码破解算法升级了
两位研究人员改进了一种著名的算法,提升了效率,可用于更大规模的密码学实验和数学计算。
数字生活愈发依赖密码学的保护。每当发送私信或网上支付时,你都在依靠算法保护数据安全。为了确保这些系统不被破解,研究人员不断测试其强度。
LLL算法(以1982年发表论文的三位研究者Arjen Lenstra、Hendrik Lenstra Jr. 和 László Lovász命名)是重要工具之一。LLL及其衍生算法有时能破解密码系统,通过研究其行为,可以设计更安全的系统。此外,该算法在计算数论等高等数学领域也有用处。
多年来,研究人员不断优化LLL算法的变体,但效果有限。最近,两位密码学家开发了一种更有效的LLL类算法,显著提升了效率。这项新技术在2023年国际密码学大会上获得最佳论文奖,将为计算机科学家和数学家使用LLL类方法拓展更多可能。
密歇根大学密码学家克里斯·佩克特(未参与论文研究)称这项技术令人兴奋,虽然研究了几十年,但仍有惊喜发现。
LLL类算法在格世界中运行,这里是指由规则排列的无限点集。可以想象你正在铺地板,可以用方形地砖,地砖的角就构成了一个格。你也可以选择其他形状的地砖,比如长平行四边形,形成不同的格。
每个格都可以用“基”描述,这是一个向量集(本质上是数字列表),通过不同方式组合这些向量,可以得到格中的所有点。例如,一个格的基由两个向量组成:[3, 2]和[1, 4]。这个格就是所有通过加减复制这两个向量的点。
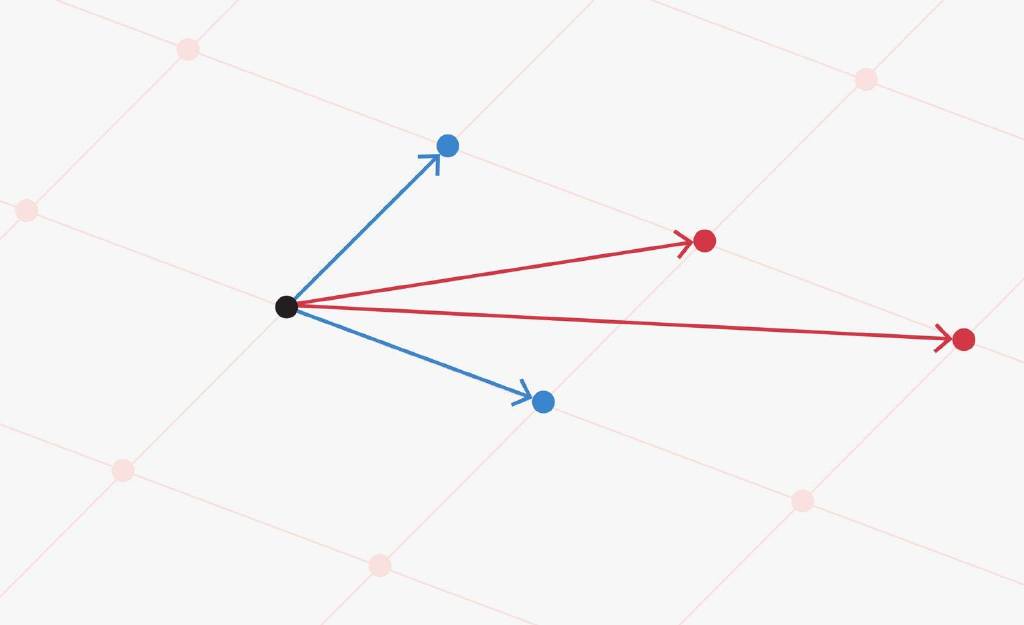
但这不是唯一的基,每个维度大于2的格都有无限多个可能的基。不过,并非所有基都一样好用。向量更短、互相近乎正交的基通常更容易处理,更适合解决某些计算问题,因此被称之为“好”基。下图中的蓝色向量就是例子。“坏”基的向量更长,也不那么正交,比如红色向量。
这就是LLL要做的事:输入多维格的基,它会输出一个“更好”的基。这个过程称为格基约简。
这与密码学有什么关系呢?在某些情况下,破解密码系统的任务可以转换为另一个问题:在格中找到一个相对较短的向量。而有时,这个向量可以从LLL类算法生成的简化基中找到。这种策略帮助研究人员攻克了一些看似与格毫无关联的系统。
从理论上讲,原始LLL算法运行速度很快:运行时间不会随输入大小(格的维度和基向量中数字的比特数)呈指数级增长。但是它会以多项式函数增加,加密研究员杜卡斯表示,如果实际操作,多项式时间并不总是可行的。
这意味着原始LLL算法无法处理太大输入。研究人员一直致力于优化LLL类算法以支持更大输入,取得了不错的效果。但一些任务仍然无法解决。
莱恩和他的导师亨宁格合著的新论文结合了多种策略来提高他们的LLL类算法的效率。一方面,该技术使用递归结构将任务分解成更小的块。另一方面,算法仔细管理涉及数字的精度,在速度和正确结果之间找到平衡。这项新工作使研究人员能够简化具有数千个维度的格基。
过去的工作也采用了类似的方法:2021年的一篇论文也结合了递归和精度管理来快速处理大型格,但它只适用于特定类型的格,并不适用于所有在密码学中重要的格。新的算法在更广泛的范围内表现良好。密码研究人员埃斯皮托说,他很高兴有人做了这件事,他们的工作提供了“概念证明”,新的结果表明“你可以非常快速地进行格约简”。
新技术已经开始发挥作用。数学家佩奇说,他和他的团队已经将改编后的算法用于一些计算数论任务。
LLL类算法还可以在设计抗未来量子计算机的格密码系统研究中发挥作用。它们不会威胁到这些系统,因为攻克它们需要找到比这些算法能实现的更短的向量。但已知最好的攻击方法将LLL类算法作为“基本构建块”,研究人员可以通过新的工具扩展可运行的攻击算法实验范围,更清晰地了解其性能。