数学家发现一种新的拓扑空间,证明了曲率与拓扑之间关系的猜想并不成立
在古老的印度寓言中,六个盲人分别触摸到大象的不同部位。他们对大象的样子争论不休:它光滑还是粗糙?它像蛇(摸到象鼻的人这样认为)还是像扇子(摸到耳朵的人提出)?如果盲人们能够结合他们的见解,他们或许能够正确地描述大象的本质。然而,他们最终却陷入了争吵。
几十年来,拓扑学家们一直希望避免落入类似的陷阱。他们认为,可以通过综合局部测量来刻画数学形状。但新发现的、具有奇异曲率的空间表明,这并不总是可能的。“事情可能比我们想象的要复杂得多,”意大利博科尼大学的埃利亚·布鲁埃(Elia Bruè)说。他与其他两位数学家合作证明了这一点。
拓扑学家们会拉伸和压缩他们研究的形状。从拓扑学角度来看,一根无限薄的橡皮筋等同于一个圆圈,因为你可以很容易地将其变形为圆形。拓扑学家倾向于根据形状的全局性质来对其进行刻画:它们是否有洞,就像一个甜甜圈?它们是否会无限延伸,就像一个无限平面,或者像球面一样“紧凑”?它们的“直线”是否会无限延伸——使它们成为数学家所说的“完备”——或者存在死胡同?
但正如寓言中的大象一样,直接感知拓扑形状的全局性质可能很困难。因此,数学家们希望了解它们与局部几何性质(如曲率)的关系。给定一个形状在每个点上的曲率信息,你能对它的全局拓扑学说什么?
1968年,当时在普林斯顿大学任教的著名数学家约翰·米尔诺(John Milnor)猜想,一个完备形状的平均曲率足以告诉我们它不可能有无穷多个洞。在接下来的50年里,许多结果支持了他的说法。“你很容易被它误导,因为它在许多现实情况下都是正确的,”纽约大学库朗数学科学研究所的杰夫·奇格(Jeff Cheeger)说。“而且,你到底该如何构造一个反例呢?”
在数学的这一领域,多伦多大学的维塔利·卡波维奇(Vitali Kapovitch)说,“米尔诺猜想可能是最大的开放问题。”
因此,在2020年,布鲁埃和他的两位同事着手证明它。他们最终找到了一个反例,并在过程中构建了一种全新的拓扑形状。“这是一项了不起的工作,”奇格说。“一个里程碑。”
拓扑学的圣杯
要理解米尔诺猜想,首先要了解拓扑学家和几何学家如何看待曲率。
两者都研究流形——在近距离观察时看起来平坦的空间。一只小蚂蚁在球面、甜甜圈或其他二维流形的表面上,会认为它所在的近邻与二维平面没有什么不同。但如果蚂蚁在任何方向稍微移动一点,它可能会注意到空间开始扭曲或弯曲。局部平坦流形的概念很容易推广到更高维度。但曲率更难定义。
例如,考虑最简单的情况:一个一维物体,如圆圈。令人惊讶的是,这些一维空间在数学意义上不能说是本来的弯曲的。沿着圆圈行走的单维几何学家,无法感知到超过一个维度的东西,会认为自己是在一条直线上旅行,并会惊讶地发现自己 retracing her steps。
但是,如果将圆圈嵌入二维平面,则显然它具有恒定的正外部曲率。(这里的相关区别在于内部和外部曲率:当你被困在空间内部时你能看到什么,与当你从外部观察时你能看到什么。)
较小的圆圈在你移动时弯曲得更快,因此具有更高的外部曲率;较大的圆圈具有较低的曲率。(从这个意义上说,一条直线就像一个无限大的圆圈。它的曲率为零,表示它完全平坦。)我们还可以将这个定义应用于具有变化曲率的更复杂形状,方法是考虑在任何给定点你需要多大的圆圈才能匹配形状。通过这种方式,曲率成为一个局部属性:流形上的每个点都具有相关的曲率。
对于一个表面——一个二维流形——有许多放置圆圈的方法,使其与表面的曲线匹配。在给定点,你可以通过在该方向放置适当大小的圆圈来测量曲率。但令人惊讶的是,可以用一个数字来定义该点表面的曲率。如果你找到在最大和最小曲率方向上给你值的圆圈,并将这些值相乘,你将得到一个称为高斯曲率的数字。这个数字以一种有用的方式总结了表面如何弯曲的信息。更令人惊讶的是,高斯曲率被证明是一个内在属性:它不依赖于表面可能被放置的任何更高维背景空间。从这个意义上说,具有奇异性的圆柱体在内部看来是弯曲的,而球体则不然。
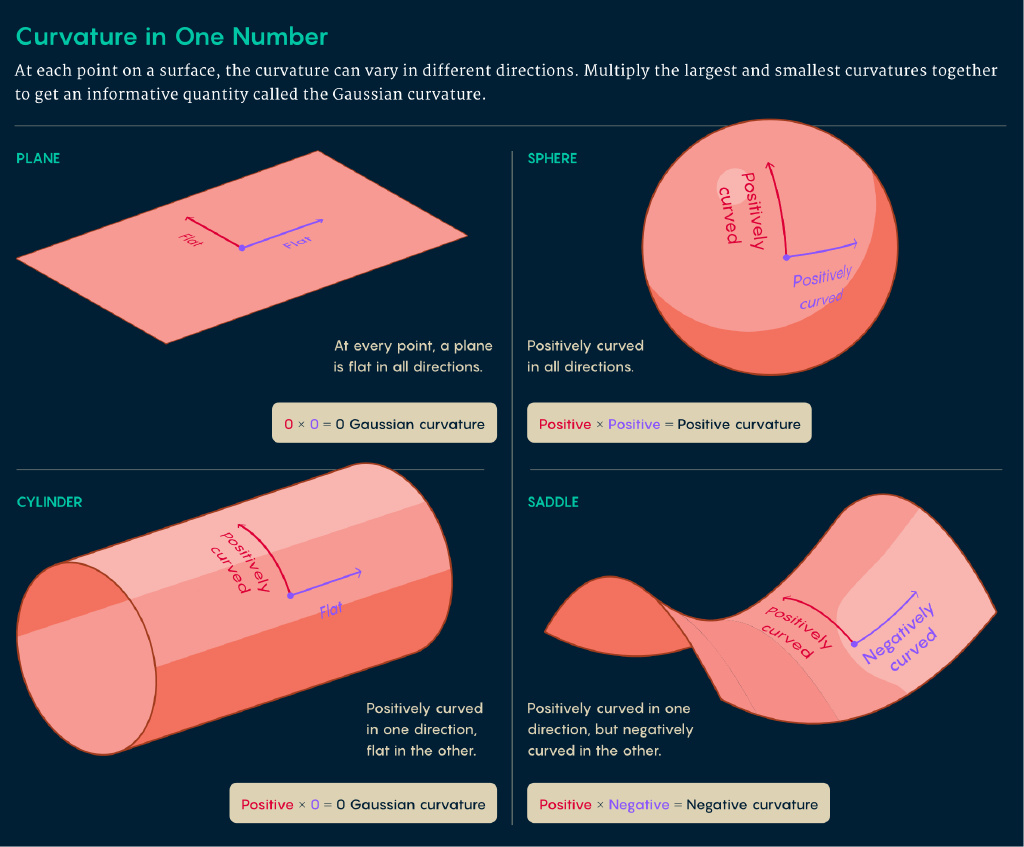
这个数字也帮助数学家们得出关于空间拓扑的结论。
例如,假设二维流形上每个点的高斯曲率都为正。那么拓扑学家可以证明它不可能有洞,就像甜甜圈一样。(它要么是标准的球面,要么是另一种更复杂的可能性。)另一方面,如果每个点的高斯曲率都为零,则存在有洞和无洞的解决方案:流形可以像无限平面一样平躺,但它也可以是圆柱体或莫比乌斯带。圆柱体与无限平面不同,它中间有一个洞。莫比乌斯带与圆柱体不同,因为它们包含扭曲。
在三维或更高维度,通常不再可能用单个数字来捕获有关曲率的有用信息。数学家们反而使用“张量”来跟踪曲率,张量可以被认为是根据特定数学规则变换的数字数组。有几种不同的方法可以使用张量来描述流形的曲率,但其中最重要的是一种称为里奇张量。与高斯曲率一样,它将必要的信息提炼成一个(相对)更简单的形式。
与数字不同,张量不能整齐地排序——但与数字一样,如果它们满足某些性质,它们可以被归类为“非负”。1968年,米尔诺猜想,里奇张量在每个点都非负的完备流形不可能有无穷多个洞(如下图右侧所示)。

半个多世纪后,布鲁埃与西北大学的亚伦·纳伯(Aaron Naber)和苏黎世联邦理工学院的丹尼埃尔·塞莫拉(Daniele Semola)一起证明了他错了。
分崩离析
当米尔诺提出他的猜想时,数学家们才刚刚开始探索里奇曲率的影响,这种曲率在数学和物理学中反复出现。“当时人们对除了定义之外的其他任何事情都知之甚少,”纳伯说。
“那时候我们在荒野中,在一望无际的平原上,只有几棵树,”奇格说。
在接下来的几十年里,数学家们填补了这幅图景,构建了例子并发展了更具体的理论。所有证据似乎都指向米尔诺猜想的正确性。
对于一维流形,这个猜想很容易证明。自1930年代以来,人们就知道它在二维空间中是正确的。2013年,它被证明在三维流形中也是正确的。如果你施加一些额外的约束——例如,假设你总是使用一个封闭和有界的流形,就像球体一样,或者其体积以特定的速率增长——那么米尔诺猜想在所有维度都成立。1978年,一位名叫米哈伊尔·格罗莫夫(Mikhael Gromov)的数学家证明,如果另一种更详细的曲率度量始终非负,那么流形只能有有限个洞。
“基本上,你假设任何事情,它都会变成真的,”纳伯说。
多年来,纳伯多次尝试在所有可能维度上证明这个猜想,而没有任何额外的假设。他失败了。后来,在2019年的一次会议上,他遇到了布鲁埃和塞莫拉,当时他们都是比萨高等师范学院的研究生,三人开始共同研究另一个问题。到2020年11月,他们解决了这个问题,布鲁埃和塞莫拉也获得了博士学位。因此,三人决定再次尝试证明米尔诺猜想。
他们坚持了超过两年。“我们试了所有我们知道的花招,”塞莫拉说。
“我们花了大量令人尴尬的时间试图证明它,”纳伯说。其中包括写了一篇80页的论文,结果证明是错误的——“这是我个人在事情崩溃之前写过的最长的一篇论文。”
但它以一种数学家们发现很有信息的但它以一种数学家们发现很有信息的 方式崩溃了。“当我们意识到这个策略有缺陷时,这让我们开始相信,也许有可能构建一个反例,”塞莫拉说。
从那以后,事情进展得更加顺利。在几个月内,三人想出了如何构造一个奇怪的七维流形。他们通过巧妙而复杂的方式将无穷多个七维部分粘合在一起,一点一点地组装他们需要的整个流形。与此同时,他们必须确保里奇曲率始终非负。他们还必须避免意外地满足米尔诺猜想已知成立的许多性质。最终,数学家们得到了一种他们称之为光滑分形雪花的东西——一种无限而精致的自相似结构。
它在每个点都具有非负里奇曲率。而且它有无穷多个洞。他们推翻了米尔诺猜想。
“它比所有先前具有非负里奇曲率的流形构造都更复杂,”加州大学圣芭芭拉分校的郭方伟说。
布鲁埃、纳伯和塞莫拉,他们都是几何学家,后来与几位拓扑学家分享了他们的工作,拓扑学家们惊讶地发现,他们创造了一种全新的拓扑空间。而且这不仅仅是因为七维有什么特别之处。使用类似的技术,三人能够在更高维空间(他们说这很容易)以及六维空间(这很困难)中构建类似的反例。目前尚不清楚四维或五维空间中是否存在反例。
由于非负里奇曲率是一个在数学和物理学中经常出现的条件,“人们希望对这些东西有一定的先天控制,”纳伯说。但事实证明,具有非负里奇曲率的形状比数学家预期的要更加灵活和不那么规则——这使得他们对局部几何性质和全局拓扑性质之间关系的理解更加复杂。
在发现新的反例之前,“你真的可以希望真正理解所有流形是什么样子,”西北大学的本·温科夫(Ben Weinkove)说。“但现在,它只是一个潘多拉的魔盒,充满了可能性。”
本文译自 Quanta Magazine,由 BALI 编辑发布。

王摸鱼2025秋款拉链卫衣