一个五百年前的数学问题探讨了圆沿直线滚动时所描绘的形状。这一被称为“循环线”的答案在多个科学领域中都找到了应用。
以下是我们“迷失在时空中”通讯的摘录。每月我们都会请一位物理学家或数学家分享他们领域中的迷人想法。你可以在这里免费订阅“迷失在时空中”。
著名艺术家Paul Klee曾将绘画形容为“带着一条线散步”——但为什么仅限于此呢?数学家们五百年来一直在思考,当圆或其他曲线“散步”时会发生什么。让我来告诉你这个迷人的故事……

想象一个轮子沿着一条路滚动——或者更数学化地说,一个圆沿着一条直线滚动。如果你追踪圆上一点的路径,它会描绘出一系列的拱形。它们的形状到底是什么?第一个认真思考这个问题的人似乎是Galileo,他给这种拱形曲线起了个名字——循环线。他对循环线着迷,其神秘之处在于看似无法回答我们对一条曲线最基本的问题——它有多长,包含多大面积?在这种情况下,直线和拱形之间的面积是多少?Galileo甚至在金属板上构建了一个循环线,以便通过称重来估算面积,但他始终未能用数学方法解决这个问题。
几年之内,似乎欧洲的每个数学家都沉迷于循环线。Fermat、Descartes、Mersenne、Newton和Leibniz都研究过它。甚至让Pascal重新回归数学,他原本因投身神学而放弃了数学。有一天晚上,他牙痛难忍,为了分散注意力,他决定思考循环线。奇迹般地,牙痛消失了,Pascal自然认为这是上帝对他进行数学研究的认可。他再也没有放弃数学。巴黎卢浮宫中的Pascal雕像甚至展示了他手持一张循环线图。事实上,这条曲线如此著名,它甚至出现在了几部经典文学作品中,如《格列佛游记》、《项狄传》和《白鲸记》中都提到了它。
17世纪中期,Roberval首次解决了循环线面积问题,答案出人意料地简单——正好是滚动圆面积的三倍。第一个确定循环线长度的人是Christopher Wren,他是一位极其优秀的数学家,不过据说他也涉足建筑。这也是一个非常简单的公式:长度是生成圆直径的四倍。循环线的魅力如此吸引数学家们,以至于它被昵称为“几何学中的海伦”。
但它的美丽并不是这个名字的唯一原因。它引发了许多激烈的争论。当数学家Torricelli独立计算出循环线下的面积时,Roberval指责他剽窃。“Roberval团队”甚至声称Torricelli因被揭穿为剽窃者而羞愧致死(尽管当时他正患有伤寒)。Descartes称Fermat关于循环线的工作是“荒谬的胡言乱语”。在回应Bernoulli的挑战时,Newton恼怒地抱怨被“外国人拿数学问题取笑”。
Huygens发现了循环线的一个惊人特性,他设计了第一个摆钟。摆钟因其运动周期——摆锤一次完整摆动的时间——恒定而成为良好的计时工具,无论释放角度如何。但实际上,这只是在近似情况下成立,周期会略有变化。Huygens想知道是否可以做得更好。摆锤末端沿着圆弧移动,但是否有一条曲线路径使摆锤无论从哪里释放都能在相同时间内到达曲线底部?这被称为“恒周期问题”。猜猜哪个曲线是解决方案?另一个附加的惊喜是它与“最速降线问题”的联系,即在任意两点间找到一个粒子在重力作用下以最短时间下降的曲线。虽然没有理由认为同一条曲线能解决这两个问题,但它确实能。答案是循环线。在完全不同的情况下遇到同一个曲线真是一个令人愉快的惊喜。
当你沿着直线滚动一个圆时,你得到的是循环线。但如果你沿着圆滚动一条直线会发生什么?这就是一种被称为“内卷线”的曲线。要画出内卷线,你将线段末端的一个点沿着曲线滚动,使其始终只是轻轻接触曲线(即切线)。内卷线是由那个点描绘出的曲线。对于圆的内卷线,想象从一个棉线卷上展开一根线,并跟随线末端的移动。结果是从圆周上出现的一条螺旋曲线。
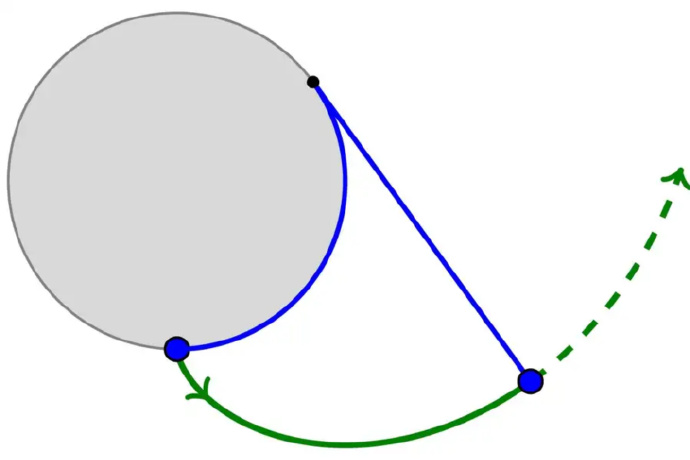
Huygens是第一个询问内卷线的人,作为他制作更精确时钟尝试的一部分。虽然知道循环线是完美的恒周期曲线,但如何让你的线绳沿着循环线路径运动?你需要找到一条内卷线是循环线的曲线。奇迹般地,循环线具有一个美丽的特性,它是自己的内卷线!但是那些美丽的螺旋圆内卷线也非常有用。
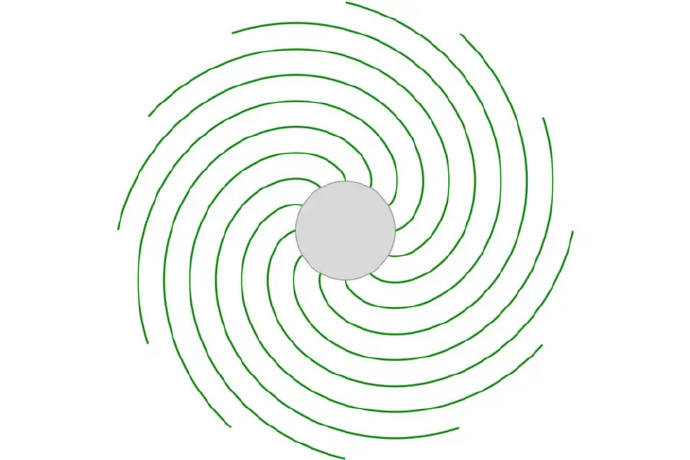
我最喜欢的应用是Huygens绝对无法预料的:在设计用于科学研究的高质量元素核反应堆时。这通过将中子高速撞击较轻的元素来创造较重的元素。在圆柱形反应堆核心中,铀氧化物燃料被夹在铝条之间,这些铝条弯曲以适应圆柱形状。每平方厘米有万亿中子在高速运动,产生的热量很大,因此冷却剂在这些条带之间流动。确保条带沿其曲面始终保持恒定距离以防止热点至关重要。这就是圆内卷线有用之处。如果你在圆周上等距画出一组圆内卷线,那么它们之间的距离沿整个曲线保持恒定。因此,它们是反应堆核心中燃料条的理想选择。更妙的是,圆内卷线是唯一能做到这一点的曲线!我喜欢这样一个最初研究用于摆钟的曲线竟然解决了核反应堆设计中的关键问题。
我们已经沿直线滚动了圆和沿圆滚动了直线。显然,下一步是沿着圆滚动圆。会发生什么呢?这里我们有一些选择。滚动圆的大小是多少?我们是在圆的内侧还是外侧滚动?沿圆内侧滚动的曲线称为内摆线;沿外侧滚动则是外摆线。如果你曾玩过图形玩具,你几乎已经画过内摆线。由于你的笔不在滚动圆的边缘,所以你实际上是在绘制所谓的内旋轮线。
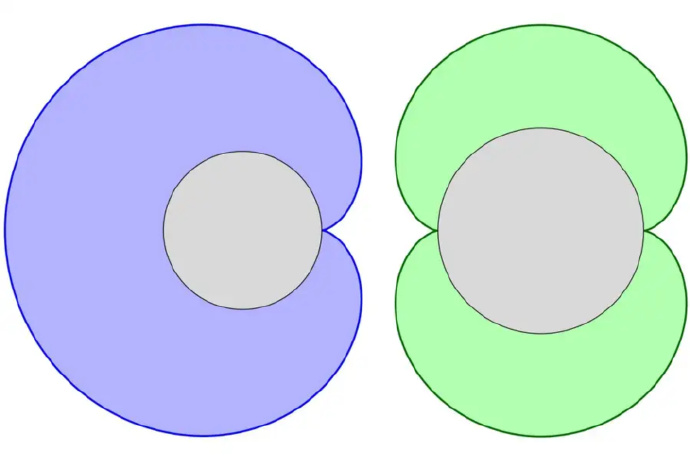
在外摆线中,最有趣的是心形线:当滚动圆的半径与固定圆相同时,形成的心形曲线。与此同时,肾形线是由半径为固定圆一半的滚动圆产生的。心形线出现在许多有趣的地方。著名的Mandelbrot集合的中心区域是一个心形线。声音工程师熟悉心形线麦克风,它们在心形区域内拾取声音。你还可能在咖啡杯中在某些光照条件下看到类似心形的曲线。如果固定光源的光线被弯曲的镜面反射,这些反射光线的切线曲线会显示为一个集中区域的光斑,称为焦散。如果光源位于一个完美圆形镜子的周边,那么结果正是一个心形线!
当然,在我们的咖啡杯例子中,光源通常不会正好在杯沿上,而是有些距离。如果它非常远,我们可以假设打在杯沿的光线是平行的。在这种情况下,可以证明焦散实际上不是心形线,而是另一种外摆线:肾形线。由于强光源在这两个极端之间,我们通常会得到介于心形线和肾形线之间的曲线。数学家Alfréd Rényi曾定义数学家为“将咖啡转化为定理的装置”。这个过程在我们美妙的外摆线上体现得淋漓尽致。
本文译自 New Scientist,由 BALI 编辑发布。
