走进科学
揭开时空弯曲的奥秘:一个简单的想象实验
想象时空是一件令人头疼的事,但数学家 Manil Suri 有一个巧妙的方法,能让你更容易理解它。
我们都熟悉空间,它有左右、前后、上下三个维度,可以把它想象成一个带有 x、y、z 轴的坐标系。时间也很好理解,它是一条永不停息的直线,每分每秒都在向前流逝。
但时空就复杂多了。爱因斯坦在他的相对论理论中将空间和时间融为一体,创造了全新的时空结构,它无处不在,甚至决定了引力的本质。爱因斯坦提出,引力不是一种神秘的远程作用力,而是由物体弯曲时空引起的。我们对宇宙的最佳描述都离不开时空。

然而,想象时空并非易事。空间的三个维度加上时间,一共四维,而且爱因斯坦还告诉我们时空是弯曲的。这意味着要真正理解它,你还需要一个第五维度的空间来容纳这种弯曲。
别担心,Suri 给我们提供了一个巧妙的办法,让我们借助一个简化的模型来想象时空。
首先,我们把空间简化为一维,这样时空的维度就变成了更容易理解的二维。然后,我们可以用一条双向水平箭头来表示这个一维空间,垂直方向代表时间,这样就形成了一个二维的时空平面。这个平面由一个个叠在一起的快照组成,每个快照都显示了物体在这一维空间中的位置。
现在,假设我们的宇宙中有两个粒子,分别位于 A 点和 B 点。如果没有引力,它们会沿着平行的直线AA' 和 BB'运动,这意味着它们在每个时间点都停留在原来的位置。
但如果引力起作用,这两个粒子会随着时间的推移相互吸引,靠近彼此。也就是说,A' 会比 A 离 B 更近。
爱因斯坦认为,引力不是一种通常意义上的力。它不会直接作用于 A 和 B 让它们靠近,而是通过改变二维时空平面来实现这一效果。那么,存在这样的变形能使 A' 靠近 B' 吗?
答案是肯定的。你可以把这个平面想象成一张橡皮布,通过拉伸它就可以制造出许多这样的变形。Suri 选择了一种特殊的变形,即把平面“包裹”成一个球体,就像把一个矩形地图投影到地球仪上一样。
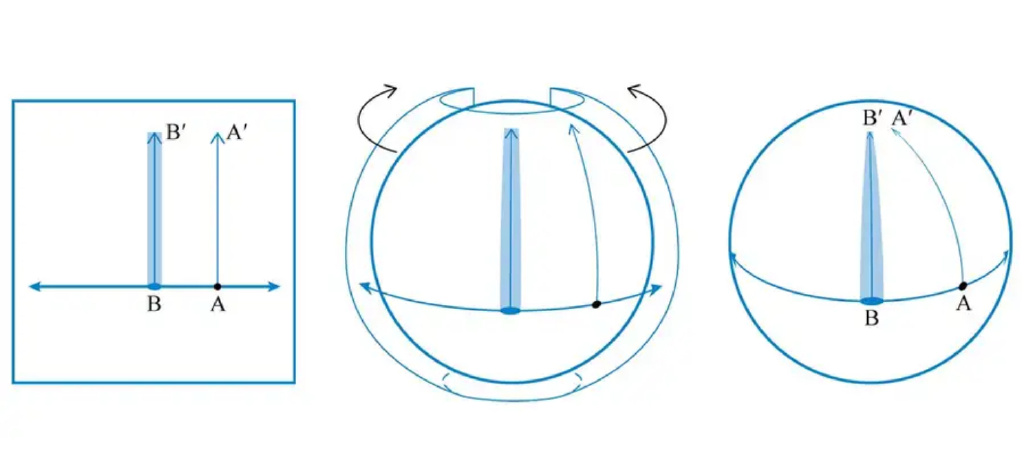
从右边的图中,你可以看到 A' 确实比 A 离 B 更近了,正符合我们对引力的理解。在平面上,粒子沿着 A 到 A' 和 B 到 B' 之间的最短路径移动,也就是直线。在球面上,AA' 和 BB' 仍然是最近距离的路径,因为球面上两点之间的最短距离总是沿着最大圆圈(例如经线和赤道)上的曲线。这些产生最短距离的曲线称为测地线。因此,平面上 AA' 和 BB' 这两条测地线在球面上也变成了相应的测地线。
爱因斯坦认为,不受外力作用的粒子总是沿着这样的“最短路径”测地线在时空移动。如果没有引力,这些测地线就是直线。引力不是一种外力,而是通过弯曲时空来改变测地线,从而让粒子沿着新的测地线移动,彼此靠近。
这就是 Suri 简化模型带给我们的关键洞察:引力不是一种神秘的超距作用力,而是时空几何的一种结果。它通过弯曲时空来吸引物体,而这种弯曲就是时空结构的一部分。
爱因斯坦正是利用这种洞察,将引力纳入了他的广义相对论。真正的广义相对论要复杂得多,因为时空只会在物体的局部弯曲,而不是像模型中那样全局弯曲。此外,这种几何还必须符合光速限制,这就意味着“最短距离”的概念也需要修改,时间维度与空间维度有本质区别。
然而,爱因斯坦的解释仍然成立。例如,太阳的质量弯曲了我们太阳系中的时空,这就是为什么行星会围绕太阳运行而不是飞出太阳系——它们只是在遵循这个弯曲时空中的测地线运动。
这种现象已经被天文学家观测到,他们看到来自遥远天体的光线被巨大的星系扭曲。这证明时空在我们的宇宙中确实存在弯曲,并非仅仅是一个数学工具。
就像一群盲人通过触摸来了解从未见过的动物——大象,时空也是如此。我们永远无法完整地看到它的四维形态,也无法直接观察它弯曲引起引力。但 Suri 提供的简化模型可以帮助我们更好地理解它。
本文译自 New Scientist,由 超载鸡 编辑发布。

