走进科学
用全等的、面积为1的瓷砖无缝铺砌二维平面,则使周长最小的瓷砖,形状为何?
思考以下问题:若用全等的、面积为1的瓷砖无缝铺砌二维平面,则使周长最小的瓷砖,形状为何?
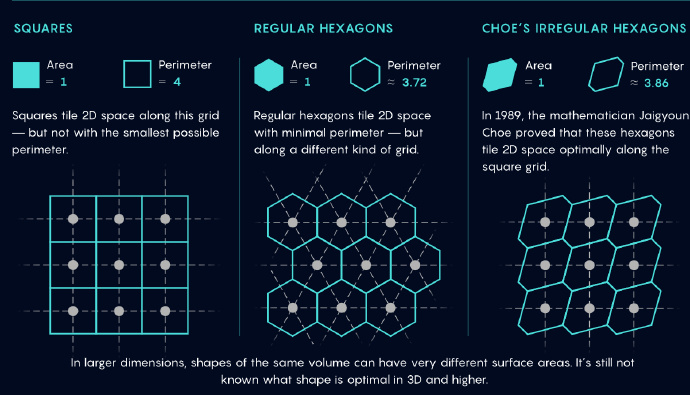
比较容易想到,单位正方形是可以满足无缝铺砌的。此时周长=4。但它满足周长最小吗?
一个常识性的内容:当面积固定时,圆是(边界)周长最小的图形。
但很遗憾,我们没法用圆盘无缝密铺平面。一个直观的思路是,更接近圆盘的多边形或许比单位正方形更加理想。事实上也是如此,可以证明,面积为1的正六边形是满足条件,周长最小的图形。
但是,若再附加一个条件:如果经过上下左右的平移,要求每个瓷砖的几何中心恰好是整数坐标点(格点)。此时,六边形就不够用了。
韩国数学家Jaigyoun Choe证明,存在最小周长为√2+√6≈3.864的瓷砖,可满足中心格点平铺平面!
思路是从常规的六边形开始,经过扭曲形变将晶格的中心转变为格点。然后调整侧面以最小化周长。
二维平面上的问题至此,完全解决。见下图:
那在三维乃至更高维度的空间里,体积为1,表面积最小的瓷砖,也不是单位立方体吗?
或者,可以仿照二维的情况,把立方体“球化”,得到表面积更小的3D瓷砖?
如果没有附加的晶格中心条件,数学家认为,一种称为Weaire-ephelan结构3D瓷砖的形状具有最小的表面积。 尽管尚未有人证明这一点,但物理实验为这一假设提供了额外的支持。 爱尔兰都柏林三一学院的研究人员在一个特殊的模具中充满了肥皂泡,发现它们自然地排成了Weaire-ephelan模式。

当附加上晶格-格点条件,长久以来数学家一直毫无思路——直到2008年左右,在一个完全没有想到的领域里,意外出现了通向答案的线索。
在计算复杂性领域里,有一个和NP完全问题相关的猜想。
之后的故事就太长了,只能长话短说。
2002年,当时还是研究生的Subhash Khot提出,如果一个特定的问题(涉及将颜色分配给网络的节点)无法准确解决,那么即使找到一个近似解决方案也是非常难的。
如果上述猜想为真,将使研究人员能够一口气理解其它各种计算任务的复杂性。这个猜想现在被称为The unique games conjecture。
几位当时在微软研究院的计算机科学家为了解决The unique games conjecture,发明了一种理论工具。在使用理论工具的过程中,他们发现需要解决的一个问题和上面的空间晶格平铺相关。
具体点说,他们期望,满足晶格平铺的瓷砖只能是立方体。
他们希望纯数学家能够解决这个几何问题,他们就能进而获得想要的结论。
但一直关注The unique games conjecture的学界强人、普林斯顿的理论计算机科学家Ran Raz反而直接从计算复杂性理论着手,直接证明,他们想要的结论是不可能达成的。
当然,微软研究院的那几位十分失望,不过组合几何领域的数学家则十分惊喜。因为这等于暗示,他们可以构造出比立方体表面积更小的、类球状的高维晶格-格点平铺。
2008年,借助Ran Raz的技术,几位数学家构造出一种高维球化瓷砖的平铺。不过,他们非常不满意,因为那个形状实在太丑陋了——甚至都不是凸的。
实际上,类球且凸的瓷砖是不存在的。
但2022年,也就是几个月前,同一拨数学家重头再来,单纯依赖几何工具,构造出了满足表面积小于立方体的凸体瓷砖。
只不过它不是球化的,而且目前凸体瓷砖的表面积要稍大于之前非凸的球化瓷砖,但数学家坚信,可以通过某些小技巧,把表面积降低到之前的数值。
理论上表面积最小的瓷砖,目前我们仍未知晓。而最新的凸体瓷砖,是否可以反哺计算复杂性理论,在不同的领域揭示更多有趣的东西吗?
诸多学者对此颇为期待。
参考
https://www.quantamagazine.org/mathematicians-complete-quest-to-build-spherical-cubes-20230210/

